计算机系统导论
1.5计算机系统性能评价
吞吐率:表示在单位时间内所完成的工作量,例如:带宽
响应时间:指从作业提交开始到作业完成所用的时间,例如:执行时间、等待时间。
存储容量:存储器存放的二进制位数,反应存储器存储能力的指标。
机器字长: CPU一次处理的二进制位,反应CPU工作能力
指令字长: 一条指令用多少位二进制数表示
存储字长: 一个存储单元能存放的二进制位数。
1.6数制相互转换
例1:
将(1010111011.0010111)2转换为八进制
001
010
111
001
.
001
011
100
1
2
7
3
.
1
3
4
例2:
将(2754.41)8转换为二进制
2
7
5
4
.
4
1
010
111
101
100
.
100
001
2.2二进制数的表示
真值:数的真实值。例如: +1011 , -1011 , +0.1010 , -0.1010
机器数:真值的符号位数字化成0表示正1表示负。例如: 0,1011 、1,1011 、 0.1010 、 1,1010
2.2.3机器数的表示
原码:等于机器数
反码:正数反码等于原码,负数反码等于原码符号位不变数值位取反。
补码:正数补码等于原码,负数补码等于反码末位加1。
2.2.4定点数和浮点数的表示
定点数概念:指计算机中的小数点位置固定不变的数的表示方式。
分类
定点整数:小数点固定在数的最低位之后。设字长为8位,能表示的数值范围为: 0000000 - 01111111即0 - (27 - 1 )
定点小数: 小数点固定在数的最高位之前。设字长为8位,能表示的范围为: 0.00000 ~ 1111111即0 - (1 - 2-7 )
浮点数概念:指计算机中的小数点位置不是固定的,或者说是“浮动”的。
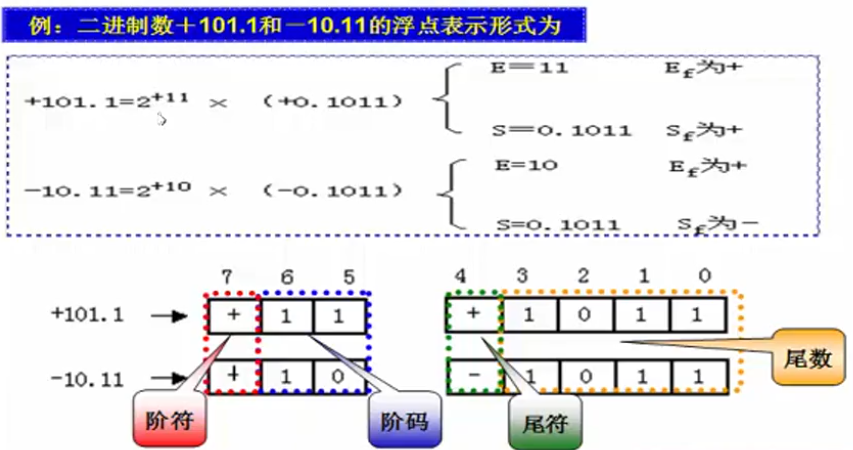
数的表示方式:通过阶码和尾数表示:N=2±E × (±S)
E称为阶码,它是一个二进制正整数;
E前的土为阶码的符号,称为阶符(Ef);表示了是扩大还是缩小,正数则为扩大,负数则为缩小
S称为尾数,它是一个二进制正小数;
S前的±为尾数的符号,称为尾符(Sf)
“2”是阶码E的底数。
2.3十进制数表示
BCD码(二进制 -> 十进制):用四位二进制代码对一位十进制数进行编码,它既具有二进制码的形式(四位二进制码),又有十进制数的特点(每四位二进制码是一位十进制数)。
例:(931)10 = (?)BCD
9
3
1
1001
0011
0001
= (1001 0011 0001)BCD
2.4字符编码
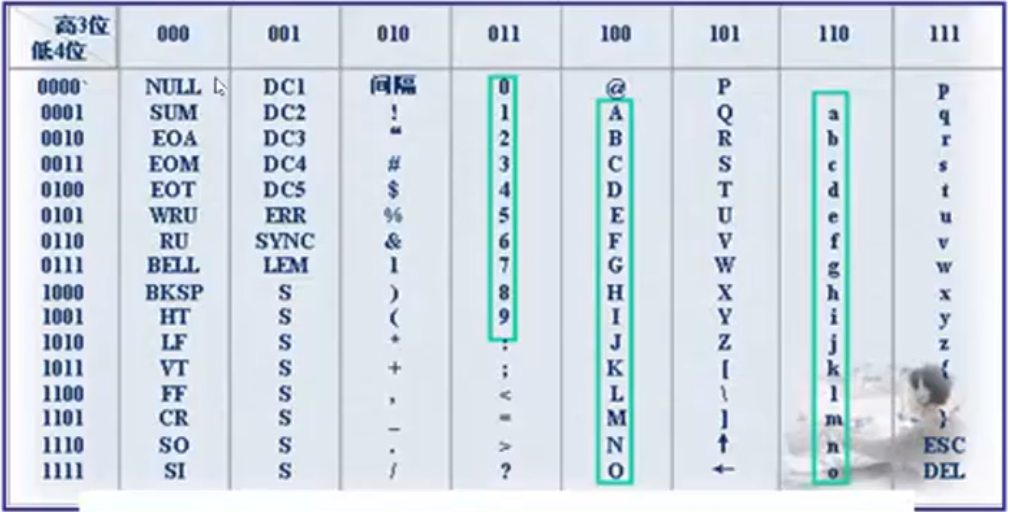
- ASCII编码:用一个字节表示,最高位置0,只用低七位,收集了128个字符和符号。当ASCII码的最高位取1时,又可表示128个字符,这种编码称为扩展ASCII码, 主要是一些制符
2.4.2 文字编码
文字编码(↓汉字的输入码(外码))
数字编码: 如电报码或国家标准GB2312 - 80规定的汉字交(国标、区位码)来输入汉字都是数字编码。数字编码法不会产生重码,但难以记忆不易推广
字音编码: 一种基于汉语拼音的编码方法。由于同音字很多,因此这种编码方法会产生很多重码
字形编码:根据汉字的字形而给出编码方法。把汉宇分解为字根、部首、偏旁、笔划等基本单位,每种基本单位与健盘上的一个健相对应,从而构成一个汉字的编码。这种输人法不易记忆但具有重码少,输入速度快等优点。
形音编码:形音编码法吸取字音编码和字形编码两种编码的特点,使编码规则简单,重码少。
汉字的机内码:是供计算机系统内部进行存储、加工处理传输统一使用的代码。目前使用最广泛的是变形的国标码将GB2312-80交换码的两个字节的最高位分别置为1而得到的。
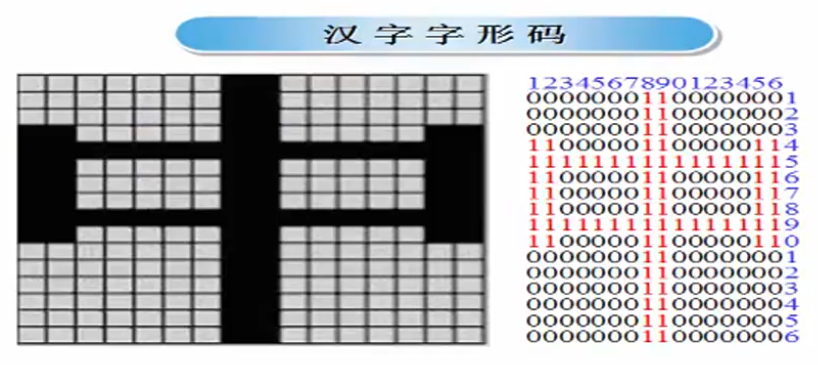
汉字字形码:是指汉字字形点阵的代码,用于汉字的显示 和打印。目前汉字字形的产生方式大多是数字式,即以点阵方式形成汉字。
汉字字库:是汉字字形数字化后,以二进制文件形式存储在存储器中而形成的汉字字模库。
2.5数据基本运算
- 算数移位
码制
添补代码
正数
原码、补码、反码
0
负数
原码
0
补码
左移 添0
右移 添1
反码
添1
逻辑位移
- 逻辑左移 低位添0,高位移丢
- 逻辑右移 高位添0,低位移丢
例如
01010011
10110010
逻辑左移
10100110
逻辑右移
01011001
算术左移
00100110
逻辑右移
11011001(补码)
2.5.3加减运算
- 加法(补码)
整数 : [A]补 + [B]补 = [A+B]补(mod 2n+1)
小数 : [A]补 + [B]补 = [A+B]补(mod 2)减法
A - B = A + (-B)
整数 : [A - B]补 = [A + (-B)]补 = [A + (-B)]补(mod 2n+1)
小数 : [A - B]补 = [A + (-B)]补 = [A + (-B)]补(mod 2n+1)连同符号位一起相加,符号位产生的进位自然丢掉
例子一
设 _A_= 0.1011 , B = -0.0101 求 [A+B]补
解:
[A]补
=
0.1011
+[B]补
=
1.1011
[A]补
+[B]补
=
10.0110
= [A]补+[B]补
注:
A + B
=
0.0110
- 例子二

3.1 程序的链接
程序的执行过程
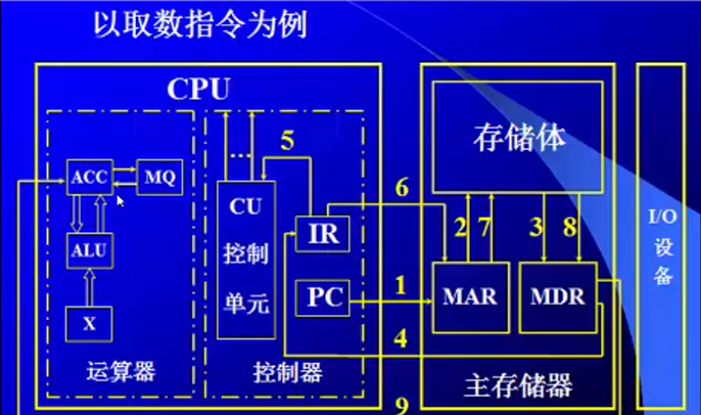
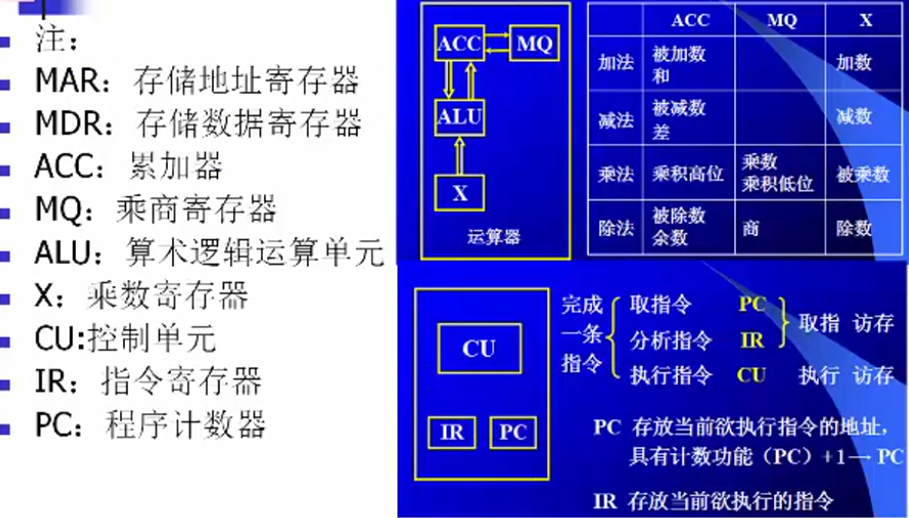
程序的执行
指令:计算机的一条命令
指令的一般格式:操作码字段 - 地址码字段- 操作码: 作何操作
- 地址吗:操作数存放的位置
寻址方式:
确定本条指令的操作数地址
下一条欲执行指令的指令地址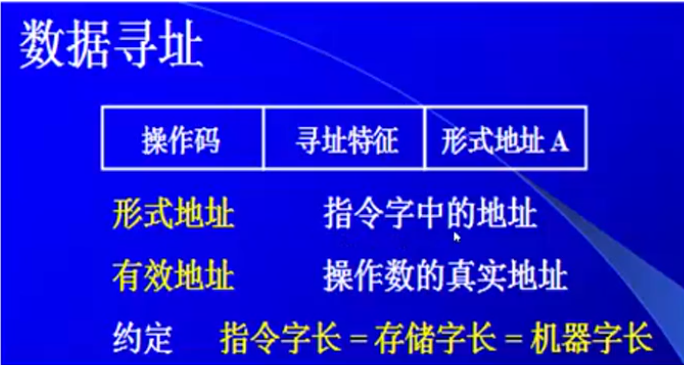
[toc]